Centroid
The centroid of a triangle is the point of
intersection of the triangleÕs three medians. A median is a segment from the
midpoint of a side to the opposite vertex. In the image below point C
represents the centroid.
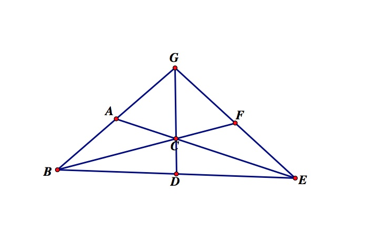
LetÕs prove that the six triangles formed by the
centroid have equal area.
We will do this by first showing that ΔBCD has the same area as ΔECD.
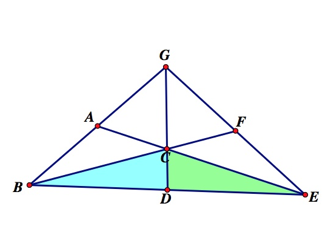
We see that the two triangles share a common side CD.
Therefore, the triangles have the same height. We also know that segment BD is
the same length as segment DE. We know this because in order to construct the
centroid D must be the midpoint of side BE. So, ΔBCD and ΔECD have the same length base and are the same
height.
By the area formula for a triangle, ![]() , ΔBCD and ΔECD are equal in area.
, ΔBCD and ΔECD are equal in area.
Applying the same ideas, we know ΔABC and ΔACG have the same
area, as well.
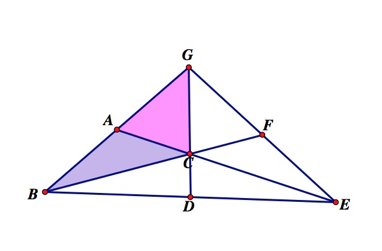
We also know the area of ΔCFG and ΔCFE will have the same area, applying the same
ideas.

Therefore, ΔBCD and
ΔECD have the same area, ΔABC and ΔACG have the same area, and
ΔCFG and ΔCFE have the same area.
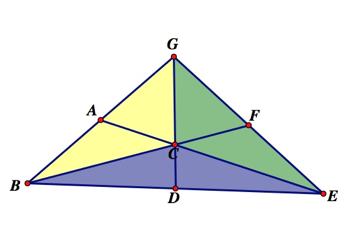
Now, we want to show that the blue region, yellow
region, and green region are all equivalent.
In order to do this we will show ΔBDG and ΔDEG have the same area.
Using similar ideas as above, since the two triangles share the side
GD we know they have the same height. We also know that the lengths of their
bases are the same since point D was constructed as the midpoint of segment BE in order to construct the centroid. Therefore, we know
their areas are the same.
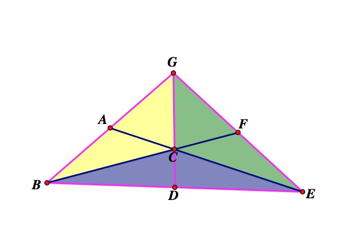
Using the abbreviations y=yellow, b=blue, and g=green,
we see,
2y+b=2g+b
2y=2g
y=g
So, a small yellow triangle has the same area as a
small green triangle.
We can apply these same properties and show ΔBFG and ΔBFE have the same area.
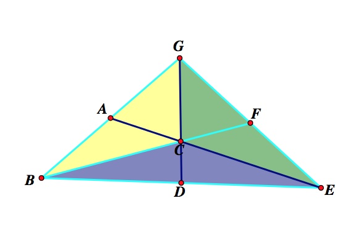
Here, we see,
2y+g=2b+g
2y=2b
y=b
So a small yellow triangle has the same area as a
small blue triangle.
So, since a small yellow triangle=a small green
triangle and a small blue triangle= a small yellow triangle, we can conclude a
small blue triangle=a small green triangle. Therefore, yellow=blue=green, and
all six triangles formed from the centroid have the same area.
For a more hands on experience, use the link provided
to learn more about the centroid.